Advertisement
In data science, two statistical approaches often guide how we interpret uncertainty: frequentist and Bayesian. You may not always realize which one you're using, but the way you model data, make decisions and explain results often reflects one of these methods. They aren't just about formulas—they reflect different ways of thinking about probability.
Whether you’re estimating future sales, testing a product change, or predicting risk, the way you use data depends on these foundations. This article looks at how these two perspectives differ and what those differences mean for your work in practical, day-to-day terms.
The biggest difference lies in how each method defines probability. Frequentist statistics view it as the frequency of an event over many repeated trials. You can’t assign probabilities to a single outcome or a fixed parameter; you can only make statements about long-run behavior. Saying a coin lands heads 50% of the time assumes endless flips, not uncertainty about the next one.
Bayesian statistics treats probability as a measure of belief. It allows assigning probabilities to hypotheses or unknowns, even before any data is collected. This belief is captured through a prior distribution, which gets updated using Bayes’ Theorem as new data comes in. That updated belief—called the posterior—reflects both prior understanding and evidence.
This change in perspective affects everything: the language used to describe results, how uncertainty is measured, and how predictions are made. Frequentist statistics tend to rely more on fixed models and repeatable processes, while Bayesian methods allow more fluid reasoning based on evolving evidence.
Frequentist inference uses sample data to estimate unknown values, assuming the true parameter is fixed but unknown. You receive point estimates, such as a mean or regression coefficient, along with corresponding confidence intervals. A 95% confidence interval doesn't mean there is a 95% chance that the true value lies within it. It means that in 95 out of 100 repeated samples, the interval would contain the true value. This interpretation often confuses outside of statistics.

Bayesian methods give you a probability distribution over possible parameter values. You start with a prior belief, combine it with data, and get a posterior. This posterior directly tells you the probability that the parameter lies within a certain range. That’s often easier to explain: “There’s a 95% probability the value is between A and B.”
The challenge with Bayesian methods is choosing the prior. If your prior is too strong or not based on real knowledge, it can bias your results. On the other hand, a well-informed prior can make your estimates more accurate, especially when data are limited.
From a practical standpoint, frequentist methods are generally easier to apply and less computationally demanding. Bayesian models, while more flexible, often require tools like Markov Chain Monte Carlo (MCMC), which can be slow and complex, especially for high-dimensional data.
The approach you choose affects more than just how you calculate results—it shapes your workflow, your model performance, and how you communicate findings.
Frequentist methods are built into most statistical and machine-learning tools. They're quick, scalable, and don't require specifying prior beliefs. A/B tests, linear regression, and classification models often rely on these assumptions. With large datasets, frequentist techniques tend to work well and produce stable estimates. When time and simplicity are priorities, this approach usually makes more sense.
Bayesian models can be more informative, especially in situations with limited data or when prior information matters. In healthcare or finance, for instance, historical knowledge is valuable and should guide analysis. Bayesian models allow this knowledge to influence the result without overpowering the new data. They’re also helpful in sequential learning, where data comes in over time and beliefs need regular updating.
Interpretation matters, too. A Bayesian model gives outputs that are more intuitive for non-technical audiences. When explaining results to decision-makers, it's easier to say there's a 70% chance something is true than to explain confidence intervals and p-values. That clarity can be a major advantage in product, marketing, and policy contexts.
The downside is speed. Bayesian methods are slower and more complex. They often need special tools and computing power. But modern libraries like PyMC, Stan, and TensorFlow Probability are improving accessibility, letting more teams use Bayesian ideas without needing advanced expertise.
There's also a growing movement toward blending the two approaches. Some frequentist models are now interpreted in Bayesian terms, while some Bayesian methods are simplified using frequentist approximations. These hybrid models offer flexibility and precision without the full cost of committing to one camp.
The decision between frequentist and Bayesian methods depends on your data and goals. With large datasets, tight timelines, or minimal need for prior knowledge, frequentist tools are usually sufficient. They’re efficient, widely supported, and reliable across many problems.

When data is scarce, events are rare, or prior knowledge is valuable, Bayesian methods are a strong option. They offer a more refined view of uncertainty and let you formally include past information, improving predictions and making conclusions easier to interpret.
Bayesian tools are becoming more accessible and faster, but using them throughout a project isn’t always practical. Many teams apply Bayesian methods selectively—like for uncertainty estimation or tuning—while using frequentist tools for most analysis.
Both methods have strengths. Frequentist approaches bring speed and simplicity; Bayesian ones offer clarity and adaptability. Knowing when to apply each—or use both—helps make better data decisions and communicate results more clearly.
Frequentist and Bayesian statistics offer different views on probability, each useful in data science. Frequentist methods are quick and work well with large datasets. Bayesian methods handle limited data better and allow prior knowledge. Neither approach is always superior; the best choice depends on the problem. As tools improve, more data scientists combine both methods in practical ways that suit real-world needs and support clearer, more flexible analysis.

How Making LLMs Lighter with AutoGPTQ and Transformers helps reduce model size, speed up inference, and cut memory usage—all without major accuracy loss

Explore the differences between the least populated countries and the most populated ones. Discover unique insights and statistics about global population distribution

How Enterprise AI is transforming how large businesses operate by connecting data, systems, and people across departments for smarter decisions
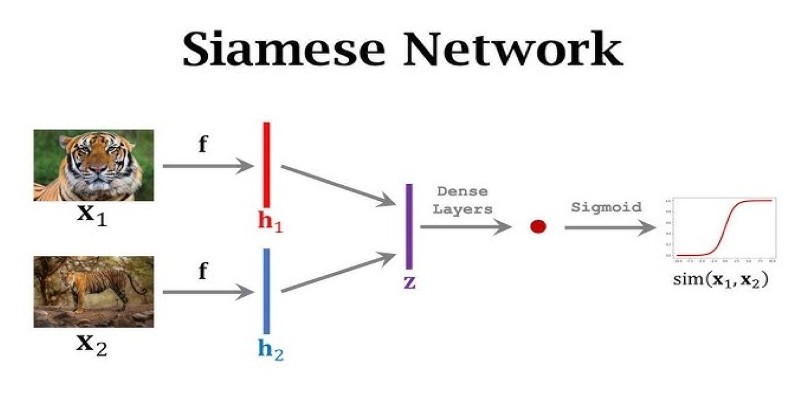
What makes Siamese networks so effective in comparison tasks? Dive into the mechanics, strengths, and real-world use cases that define this powerful neural network architecture
Explore the most unforgettable moments when influencers lost their cool lives. From epic fails to unexpected outbursts, dive into the drama of livestream mishaps

What data management is, why it matters, the different types involved, and how the data lifecycle plays a role in keeping business information accurate and usable

How Würstchen uses a compressed latent space to deliver fast diffusion for image generation, reducing compute while keeping quality high

How to use transformers in Python for efficient PDF summarization. Discover practical tools and methods to extract and summarize information from lengthy PDF files with ease

Deploy models easily and manage costs with the Hugging Face Hub on the AWS Marketplace. Streamline usage and pay with your AWS account with-out separate billing setups

Discover the top ten tallest waterfalls in the world, each offering unique natural beauty and immense height
How Fetch cuts ML processing latency by 50% using Amazon Sage-Maker and Hugging Face, optimizing inference with async endpoints and Hugging Face Transformers

Learn the clear difference between data science and machine learning, how they intersect, and where they differ in purpose, tools, workflows, and careers